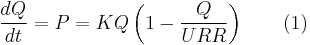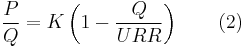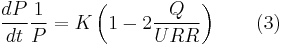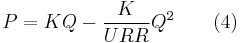Hubbert Linearization
The Hubbert Linearization is a way to plot production data to estimate two important parameters of a Hubbert curve; the logistic growth rate and the quantity of the resource that will be ultimately recovered. The Hubbert curve is the first derivative of a Logistic function, which has been used in modeling depletion of crude oil, predicting the Hubbert peak, population growth predictions[1] and the depletion of finite mineral resources[2]. The technique was introduced by Marion King Hubbert in his 1982 review paper [3]. The geologist Kenneth S. Deffeyes has recently applied this technique to make a prediction about the peak production of conventional oil [4].
Contents |
Principle
The first step of the Hubbert linearization consists of plotting the production data (P) as a fraction of the cumulative production (Q) on the vertical axis and the cumulative production on the horizontal axis. This representation exploits the linear property of the logistic differential equation:
where K and URR are the logistic growth rate and the Ultimate Recoverable Resource respectively. We can rewrite (1) as the following:
The above relation is a line equation in the P/Q versus Q plane. Consequently, a linear regression on the data points gives us an estimate of the slope and intercept from which we can derive the Hubbert curve parameters:
- the K parameter is the intercept with the vertical axis.
- the line slope is equal to -K/URR from which we derive the URR value.
Examples
US Oil Production
The chart on the right gives an example of the application of the Hubbert Linearization technique in the case of the US Lower-48 oil production. The fit of a line using the data points from 1956 to 2005 (in green) gives a URR of 199 Gb and a logistic growth rate of 6%.
World Population
Alternative Techniques
Second Hubbert Linearization
The Hubbert linearization principle can be extended to the second derivatives[5] by computing the derivative of (2):
the left term is often called the decline rate.
The Hubbert Parabola
This representation was proposed by Roberto Canogar[6] and applied to the oil depletion problem:
See also
References
- ^ Roper, David. "Projection of World Population". http://arts.bev.net/roperldavid/WorldPop.htm.
- ^ Roper, David. "Where Have All the Metals Gone?" (PDF). http://www.roperld.com/minerals/metalgon.pdf.
- ^ "Techniques of Prediction as Applied to the Production of Oil and Gas", in the collection Oil and Gas Supply Modeling, edited by Saul I. Gass (published as NBS Special Publication 631)
- ^ [|Deffeyes, Kenneth] (February 24, 2005). Beyond Oil - The view from Hubbert's peak. Hill and Wang. ISBN 978-0809029563.
- ^ Khebab (2006-08-18). "A Different Way to Perform the Hubbert Linearization". The Oil Drum. http://www.theoildrum.com/story/2006/8/16/102942/337.
- ^ Canogar, Roberto (2006-09-06). "The Hubbert Parabola". GraphOilogy. http://graphoilogy.blogspot.com/2006/09/hubbert-parabola.html.
External links
- Does the Hubbert Linearization Ever Work? - The Oil Drum
- Hubbert's Peak, The Coal Question, and Climate Change - Peak Oil, Peak Coal, Peak fossil-fuels]
- Excel Workbook - Hubbert's Peak, The Coal Question, and Climate Change